Согласно теореме, пусть h количество хорд окружности. Тогда они разобьют круг на (h + 1) частей (рис. а). Но если имеются пересечения хорд, то общее количество разделенных областей окружности (рис. б) составит
M = 1 + h + t, где t – число точек пересечения.
Две точки на окружности образуют хорду, то количество проведенных хорд равно h = n(n – 1)/2 или согласно индукции h = С²n (рис.в). Через каждые четыре точки на окружности можно провести только две пересекающиеся хорды (рис. г). В результате, число пар пересекающихся хорд, равно числу способов выбрать четыре точки из n. Тогда t = C⁴n = n(n - 1)(n - 2)(n - 3)/24. Таким образом, хорды поделят окружность на следующее количество частей
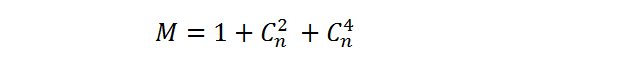
Вот вычисленные значения для девяти вариантов, где - первое число количество точек, второе – долей окружности: 1 – 1, 2 – 2, 3 – 4, 4 – 8, 5 – 16, 6 – 31, 7 – 57, 8 – 99, 9 – 163. При сравнении результатов, имеем несовпадение частей у «шестиугольника»: 31 против 30, указанных в условии. Дело в том, что автор вопроса предоставил рисунок с равномерным распределением точек по окружности, которые являются вершинами правильного многоугольника с четным количеством сторон. Поэтому в центре окружности имеем пересечение трех хорд в одной точке, что явилось причиной потери одной части окружности (рис. д). Например, при восьми точках на окружности, образующих правильный многоугольник, недосчитаемся 11 частей. Следовательно, формула верна, если никакие три или более хорд не проходят через одну точку.